Laser
The word laser is an acronym for Light Amplification by the Stimulated Emission of Radiation.
For a simple explaination about LASERs read How Do LASERs work? Information about Types of Lasers can be found here.
Contents
Laser properties
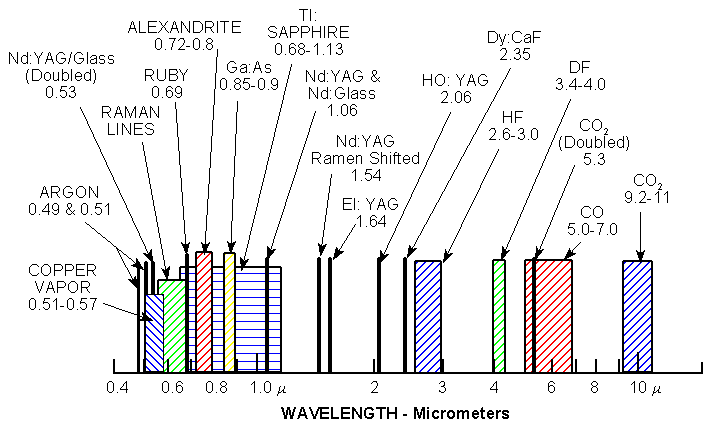
Color
The color of a laser is related to the physics of the lasing medium. Holography grade lasers are made in almost every color of the rainbow from UV to IR. The most common colors (lines) used for holography are 650nm red (laser diodes), 633nm (Helium-Neon Lasers), 532nm (frequency doubled Yag DPSS lasers) , 514nm and 488nm (argon lasers).
Power
Power is the measurement of the energy contained in the beam. For continuous wave lasers (CW) is is measured in milliwatts (mw) or watts (W). The more power a laser has the shorter the exposure time will be, and consequently, the less stringent the constraints on table stability are. While it is possible to create holograms with laser powers of 1mW and less, 5mW or more is recommended in order to have conveniently short exposure times for usual film sizes. On the other hand, going much beyond this power level creates a severe danger for the eyes; in principle, one should always use as little power as necessary for a given application.
Typical power levels of HeNe lasers are 1-20mW, of diode lasers: 5-50mW, of DPSS lasers: 20-200mW, and of argon lasers with etalon: 100-500mW. But, if the money is no object powers of over 1 watt can be obtained in Argon and DPSS lasers.
The power for pulsed lasers is measured in Joules. Most holographic Pulsed laser systems fall into the .1 to 10 Joule range and are of a MOPA design and either Frequency Doubled ND:YAG/ND:Glass lasers or Ruby Lasers.
Divergence
Laser beams do not stay the same diameter as they travel. They expand and the rate of the expansion is measured in millirads. The divergence of a laser is of little importance to holography. However when blending lasers of different frequencies for color work it is important to match the divergences.
Polarization
While any polarization state will make a hologram a polarized laser will make the most efficient holograms. Lasers are usually classified as either non-polarized or a polarization ratio is specified like 100 to 1. When a laser is listed as non-polarized it means that there are no optics to set the polarization angle. This does not necessarily mean the beam is not polarized but often that the polarization of the beam rotates as time passes.
In order to set the polarization of a laser there needs to be a polarizer in the cavity. The most common polarizer is an optic set at the Brewster's Angle. I can be one of the cavity mirrors or a window in the cavity.
Transverse Modes
This image shows the modes for polarized lasers.
A laser for holography needs to be TEM00. This stands for Transverse Electric Mode. It is a measure of how even the laser beam is in cross-section. Using a laser with a higher order mode makes it impossible to get even illumination, and also the individual spatially distinct beam components may not be in phase with each other (ie, cannot interfere to form a hologram).
A TEM00 beam has a Gaussian distribution.
Longitudinal Modes and Coherence Length
Besides various Transverse Modes, a laser can also emit various longitudinal modes which have just slightly different wavelengths. This is because the resonance condition can be satisfied by many different wavelengths. That is, assuming the laser resonator has length L, it allows all modes to be present whose wavelength lambda satisfies L= N lambda/2, where N is an integer. So if lambda is very small (like 600nm) and the condition is satisfied by some very large N, then it is also satisfied by a slightly different lambda and a slightly different N. The frequency difference of two adjacent modes is called mode spacing and given by delta_f = c/(2L).
In practice, the laser material won't amplify any possible resonance mode, but only frequencies that lie within a certain gain window, so at most a few longitudinal modes will be able to lase. With special methods, like using an etalon, one can achieve a clean single frequency operation.
The presence of more than one longitudinal mode is a serious obstacle against recording holograms with significant depth. The reason is that when several modes with slightly different wavelengths are present, they will be out of phase after having traveled a certain distance D. The quantity D is customarily called coherence length. It leads to a blurring of the interference fringes when the path difference between object and reference beam becomes comparable to D. In other words, the maximal recordable depth of a hologram is in the order of D.
If one has a single longitudinal mode, then D is essentially "infinite". In practice, it is then governed by the line width of the laser emission, and this can be very small (like one Mhz, which corresponds to D=150m). When two or more modes are present, then their frequency difference delta_f is what dominates the coherence length. The mode spacing is generally given by the resonator length L, so if two modes are present, then the coherence length is approximately D=L. If three are present, then the frequency difference between the most distant modes is twice as large as before, so D=L/2. And so on... if M modes are present, then the coherence length is approximately D=L/(M-1) (this assumes, for simplification, that all the modes have equal strength).
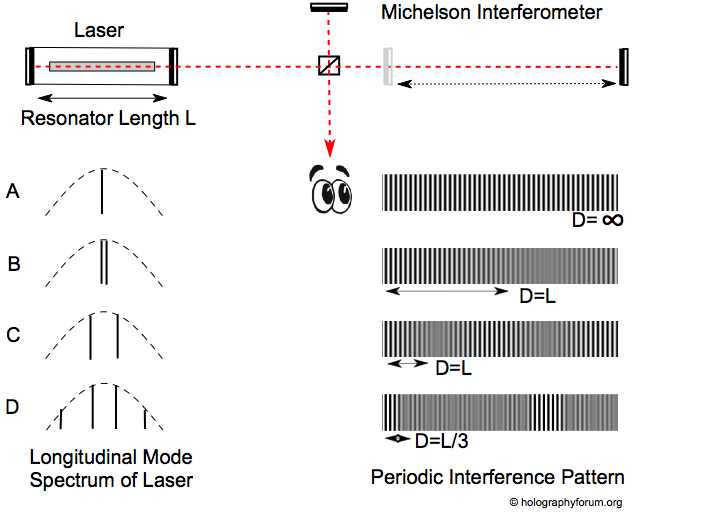
All this is illustrated by the following figure. The coherence length is measured by a Michelson Interferometer, and given by the maximal path length difference where reasonable fringe contrast occurs. On the left various laser spectra with different longitudinal modes are shown (the dashed line symbolizes the gain profile). On the right, shown are the corresponding interference patterns that arise when translating the movable mirror (mathematically speaking, they display the Fourier transformation of the spectrum). The important point is that the fringes blur in a way that depends on the details of the laser spectrum.
The following scenarios are shown:
- A: Single frequency operation - the coherence length D is basically infinite.
- B: Two modes oscillate, so the coherence length D is basically L. Assumed is that the lines are quite close (L is large).
- C: Again two modes oscillate, so again D=L. But here L is assumed to be small, resulting in a shorter coherence length than before.
- D: Four modes oscillate, so D=L/3 is quite a bit shorter than before. This scenario is typical for powerful lasers with a lot of gain.
For example, for a Helium Neon laser, the gain window is typically 1Ghz. Assume the resonator length is L=60cm, then its mode spacing is c/(2L)=250Mhz. Thus up to four modes can be present simultaneously, and if this is the case, then D=60(4-1)=20cm. This is a reasonable value for recording most holograms.
For an argon laser, due to the high plasma temperature the gain window is like 10Ghz. Assuming again that L=60cm, up to 40 modes can simultaneously lase, and the coherence length will be approximately D=60cm/39~1.5cm. This allows to record only very shallow holograms! Thus, an etalon is pretty much required.
For a diode laser, the resonator length is very small, and the mode spacing can be 100Ghz. This means that the moment two or more modes lase, the coherence length drops down to a fraction of an inch. Thus, multi-frequency operation of a diode laser must be avoided by all means!
In practice, the way to the determine longitudinal mode structure and coherence length of a laser is either by setting up a Michelson Interferometer as shown above, or by directly displaying the laser spectrum by a scanning Fabry-Perot interferometer. See Sam's and W' notes on home-built SFPI's. For diode lasers with a large mode spacing, the longitudinal spectrum can be most conveniently displayed by a grating based optical spectrum analyzer with sufficient resolution (better than approx 0.2nm). Such a device can be build in a simple manner by using a CD or DVD as grating, in combination with a path length of several meters.
I had to add this example for calculating coherence length from the forum.
From Iovine's "Homemade Holograms" p. 154:
If you know the range of frequencies:
CL = c / (2 * range in Hz) - c is speed of light in m/sec
For a range of wavelengths:
CL = (center wavelength in meters)^2 / (2 * range in meters)
Example: laser diode at 670 nm with wavelength range of 0.2 nm should have a CL of (670 * 10^-9)^2 / 2 * (0.2 * 10^-9) = 0.0011 meter.
Mode Hops
There are often a number of sable longitudinal modes that can exist in a laser cavity. If the laser jumps from one to the next it is called a Mode Hop. A Mode Hop will destroy a holographic image causing "banding" or "sliced bread" holograms.
Known Lasers that work for Holography
- Spectra Physics Model 164 with prism (single line operation) and etalon (added coherence)
- Spectra Physics Model 165 with prism (single line operation) and etalon (added coherence)
- Infiniter 200 Laser Pointer
- Integraf Laser Diode
- Coherent C315 DPSS 532nm
- Lexel 85 Argon Laser with wavelength selector and Etalon
- Lexel 95 Argon Laser with wavelength selector and Etalon
- Most tubular black casing HeNe lasers
More information about Types of Lasers is available here.
A most detailed discussion of lasers for the amateur can be found in
Sam's Laser FAQ.